The High Current Experiment (HCX) at LBNL is primarily designed to study the transport of high current beams at the low energy end of a Heavy Ion Fusion (HIF) driver. Two new diagnostics, an electrostatic Energy Analyzer (EA) and a Time of Flight pulser (TOF) were installed to more precisely determine the beam energy and to make longitudinal phase-space measurements.

The EA, a 90° spectrometer with a radius of 46 cm, and a gap of 2.5 cm was operated up to ΔV = 110 kVor delta V= 110 kV. The relative accuracy is ± 0.2%, allowing us to follow variations in the beam energy as a function of time during the beam pulse.  The EA calibration depends on the geometry and fringe fields of the analyzer. By changing the beam energy by a known absolute amount, we provide an independent calibration. The beam passed through a 28%-transparent hole-plate, and the gas cloud created at the hole-plate stripped singly-charged K⁺ beam ions to doubly-charged K²⁺. The absolute calibration was determined by varying the electric potential at the plate, and thus the energy of the K²⁺ ions entering the EA.

TOF measurements were made by inducing short-duration (0.3 μs FWHM), small-amplitude (~10 keV) energy perturbations in the matching se ction using a specially designed fast pulser. These energy pulses were manifest as current perturbations measured ~5 m downstream. Figure 1 shows a close-up of the beam current waveform measured downstream along with a theoretical calculation of the expected perturbation based on a 1-D cold-fluid model. Comparing the measured and expected delay time of the perturbation determines the absolute energy of the beam.
 
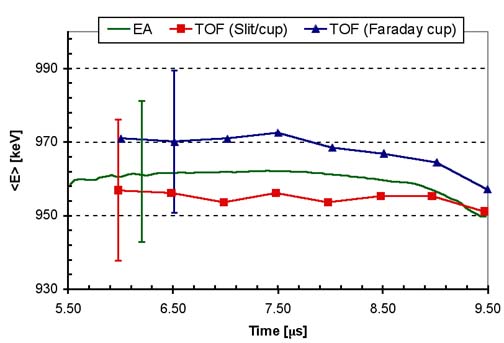
Both the TOF an EA diagnostics determine the absolute beam energy to ±2%, with both measurements agreeing within these uncertainties (Figure 2). The precise determination of the energy  is essential for agreement between simulations and experimental data.

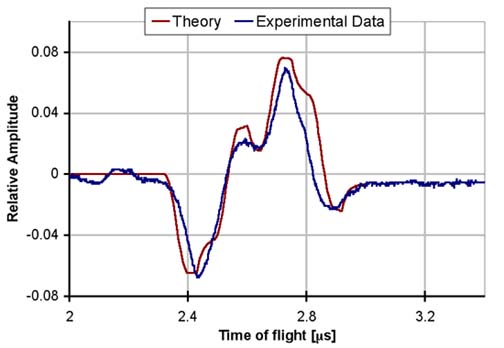
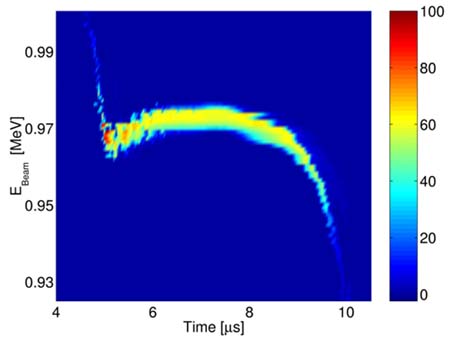
Figure 3 shows the longitudinal energy distribution obtained with the EA. The high-energy head and low-energy tail are understood to be from the beam longitudinal space charge, which accelerates particles at the front end of the bunch and decelerates particles  at the rear of the pulse. These data also show that in the middle of the pulse, the mean beam energy is constant to within 0.5% for 3.1 ms.

Figure 1 – Cold fluid model vs TOF
 perturbation on the beam current
waveform. Perturbation applied @ t = 0.

Figure 2 – TOF and EA measurements comparison.
The error bars represent the systematic error (± 2%).
 

Figure 3 – Longitudinal Energy
Distribution measured with the
 electrostatic energy analyzer.

Study of mismatch oscillations in beam envelope

Mismatch oscillations, in the envelope of beam particles, play a role in transport limits by generating halo. This induces beam loss, resulting in gas desorption and secondary electron production, so understanding mismatch oscillations are  important in the transport of intense ion beams. We performed an extensive analytical and numerical study on the transverse envelope oscillations of intense ion beams in continuous focusing, periodic solenoidal, and periodic quadrupole transport channels. This study significantly extends earlier work by Struckmeier and Reiser [Part. Accel. 14, 227 (1984)] and is being submitted for publication. We map regions of parametric instability, find new classes of envelope instabilities, explore parametric sensitivities, describe launching conditions for pure normal mode oscillations, and calculate analytically accessible limits. 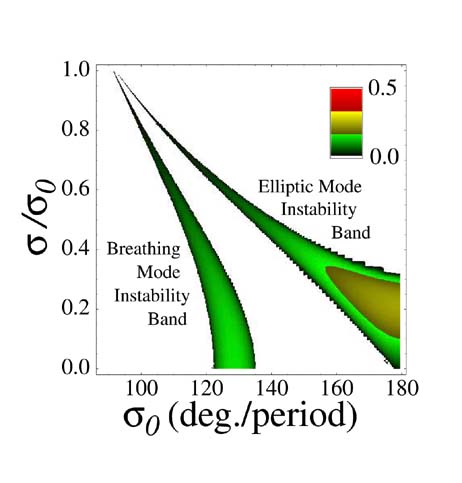We also analyze driving sources of mismatch oscillations resulting from focusing errors, particle loss, and beam emittance growth. The figure shows bands of parametric instability for breathing and elliptical envelope distortions for a periodic solenoidal focusing lattice with  solenoids  filling 75%  of  the lattice. If higher order  instabilities  can also be  suppressed,  broad  parameter  regions  with σ₀ >90° or sigma₀ >90 degrees outside of the envelope instability bands can be exploited to allow transport of higher current density beams.
 

Figure 1 – Contours of the log of 
the growth in envelope oscillation
amplitude per lattice period for
periodic solenoid focusing as a
function of the single particle phase 
advance σ0 or Sigma0 and the space-charge
depressionσ/σ0 or Sigma/Sigma0.